Evaluation Metrics¶

RMSE¶

Root Mean Square Error (RMSE) is a frequently used measure of the differences between values (sample or population values) predicted by a model or an estimator and values observed, and its formula is given as follows:

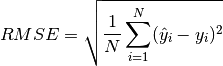
$RMSE=\sqrt{\frac{1}{N}\sum_{i=1}^{N}(\hat{y}_i-y_i)^2}$

where 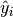$\hat{y}_i$ denotes the value predicted by a model, 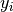$y_i$ denotes the observed values.

MAE¶

Mean Absolute Error (MAE) is a measure of errors between paired observations expressing the same phenomenon.

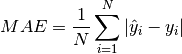
$MAE=\frac{1}{N}\sum_{i=1}^{N}|\hat{y}_i-y_i|$

where 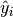$\hat{y}_i$ denotes the value predicted by a model, 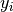$y_i$ denotes the observed value.

R-squared¶

R-Squared (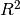 $R^2$ ) also known as coefficient of determination, is usually used in the context of statistical models whose main purpose is either the prediction of future outcomes or the testing of hypotheses, on the basis of other related information. 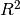$R^2$ is usually determined by the total sum of squares (denoted as 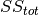$SS_{tot}$ ), and the residual sum of squares (denoted as 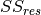$SS_{res}$ ), and its formula is as follows:

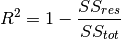
$R^2 = 1 - \frac{SS_{res}}{SS_{tot}}$

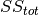$SS_{tot}$ is calculated as follows:

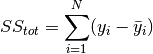
$SS_{tot}=\sum_{i=1}^{N}(y_i-\bar{y}_i)$

where 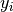$y_i$ denotes the observed value, 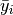$\bar{y}_i$ denotes the average values of all observed values.

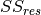$SS_{res}$ is calculated as follows:

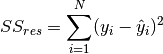
$SS_{res} = \sum_{i=1}^{N}(y_i - \hat{y}_i)^2$

where 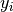$y_i$ denotes the observed value, 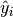$\hat{y}_i$ denotes the predicted value.

Explained Variance¶

Explained Variance is used to measure the discrepancy between a model and actual data. Its formula is given as follows:

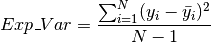
$Exp\_{Var} = \frac{\sum_{i=1}^{N}(y_i-\bar{y}_i)^2}{N-1}$

where 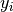$y_i$ denotes the observed value, 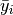$\bar{y}_i$ denotes the predicted value.

AUC¶

Area Under Curve (AUC) usually used in classification analysis in order to determine which of the used models predicts the classes best. In recommender systems, AUC is usually used to metric for implicit feedback type recommender, where rating is binary and prediction is float number ranging from 0 to 1. For more details, you can refer to Wikipedia.

LogLoss¶

Log Loss also known as Cross-Entropy Loss, its discrete formal is given as follows:

$LogLoss=-\frac{1}{N}\sum_{n=1}^{N}[y_n\log\hat{y_n}+(1-y_n)\log(1-\hat{y_n})]$

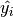where $\hat{y_i}$ represents whether the predicted result is positive.